Following on from my last article (below) on how too much content damages both thinking and learning, I’d like to address a question that we seem to keep cycling back to: what makes a curriculum “rigorous”?
A couple of similar terms routinely appear in the discourse on rigour, usually as a call to return to the ‘good old days’ of education—you know, back when we did everything right… These terms include robust, knowledge-based; maybe challenging or comprehensive.
There’s certainly something ‘no nonsense’ about these. Like we’ve sorted out all the chaff and are finally bring some common sense to curriculum design (and, of course, purging any vestiges of wokeness, the all-pervasive fear of pearl-clutchers and outrage merchants).
But let’s be very careful what we wish for, because, in education at least, rigour can have very different meanings.
Two flavours of ‘rigorous’
Here’s two ways to think about ‘rigorous’, expressed as clutches of associated terms (we could add more, but you get the idea).
Careful, thorough, thoughtful, considered, consistent, challenging, demanding, conscientious, diligent, attentive, precise, exacting, accountable, methodical.
Strict, adhering, compliant, exhaustive, pedantic, stringent, inflexible, uncompromising, intransigent, rule-bound, procedural.
These two grouping express ends of a continuum. One (1) is rich, deep, complex, multifaceted and deeply engaging. The other (2) is, well, less so. I’d like to call these the purposeful-generative and the procedural-restrictive conceptualisations of rigorous, but that’s a mouthful. I’m going to strip it down to generative and restrictive instead.
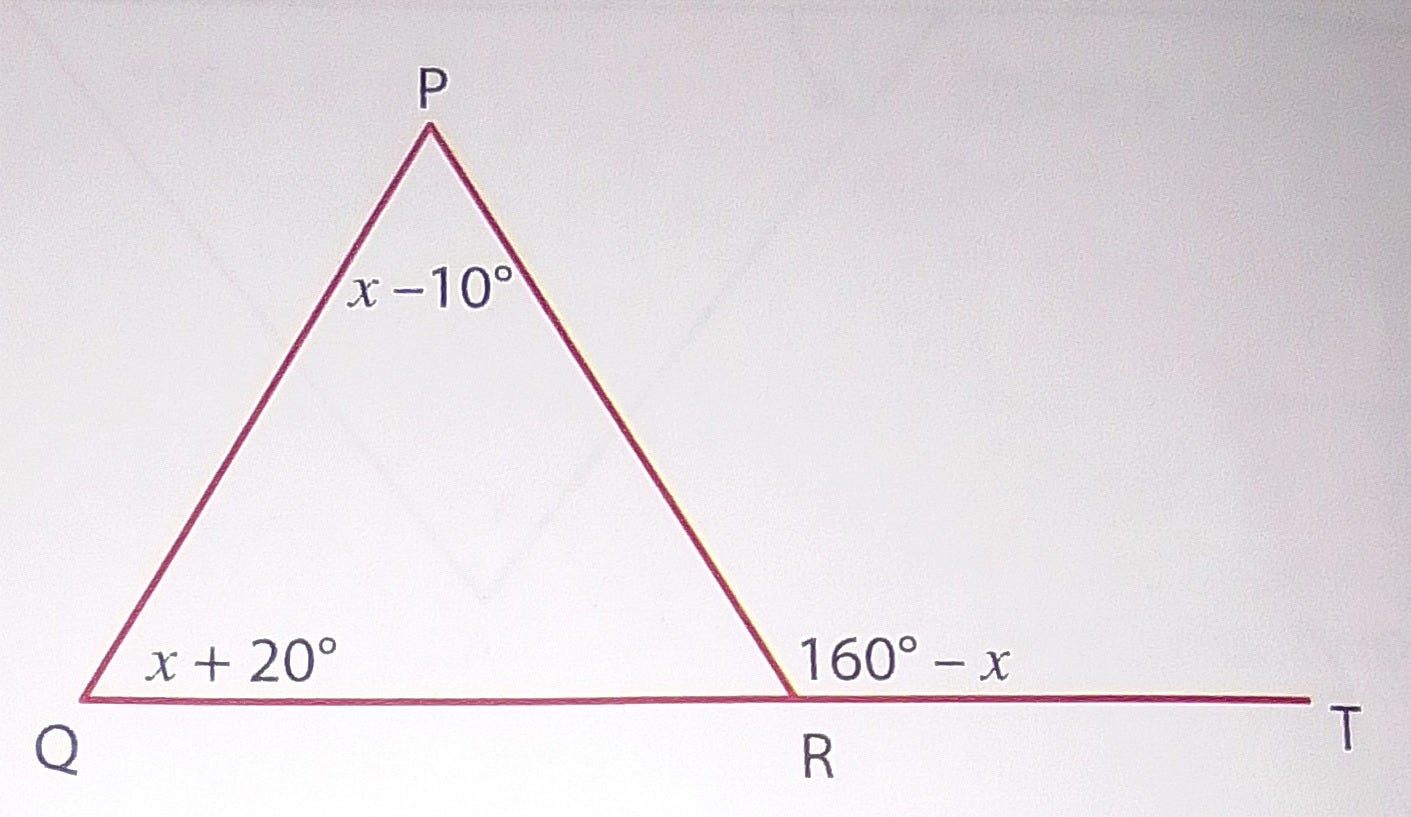
These variations of rigour are reflected in the types of problems we give students. We can think of ‘well-structured’ problems as those with very few ways to do them, and often only one. Here is a classic example from geometry, in which there is only one answer and a limited number of ways to get to it: Find the value of x.
Bringing a few simple rules together and using some basic algebra, the answer falls out pretty algorithmically. This problem is adequately—perhaps most efficiently—approached from a restrictive stance. Why would you teach it any other way?
Such problems can range from the simple (as above) to the complex. As a Physics teacher of many years, I am very familiar with ranging my problems to students from simple to complex while keeping them restrictive in approach.
Contrast this problem with the following: Are octopuses intelligent? Simple enough question to ask, but think about what students might need to do to answer it.
First comes the question of what we might mean by ‘intelligent’. Could there be different ways of understanding intelligence? Might it be possible for intelligent species to pass like ships in the night, each unaware of the others manifestation? And then, how could we test for intelligence, even if we restricted it to familiar patterns? And is it linked to emotional behaviour, self awareness or just problem-solving? And what kinds of problems?
There’s a lot to unpack here. Many ways in which we could go forward and many ways of framing our inquiry. And it’s possible we might end up at different but equally worthy conclusions, so long as we could justify our thinking and our methods.
We start the geometry problem with a clear understanding that the answer exists, and is singular. Not so the octopus problem, which is characterised by doubt and ambiguity. It is a good example of a generative approach. Students need to generate lines of inquiry and make progress along a clear vector of improvement fixed by the overarching question. It is much messier and more consciously directed than most restrictive approaches.
The octopus problem is what we call in the literature ‘ill-structured’. It’s not a pejorative term, it just speaks to the openness of the inquiry process. The geometry problem is a ‘well-structured’ one. Generally speaking, well-structured problems are restrictive in their approach, ill-structured problems are generative.
Degrees of freedom of inquiry
I’ve noted that sometimes there is a limited number of ways to approach a problem, and other times there can be many. I identify this variation using the idea of degrees of freedom of inquiry. The more degrees of freedom, the greater the potential courses of action open to us. Well-structured problems usually have fewer degrees of freedom that ill-structured problems.
When we have doubt, ambiguity and uncertainly, when we have potentially many degrees of freedom in our inquiry, these are the times when a restrictive approach is insufficient and a generative approach is necessary.
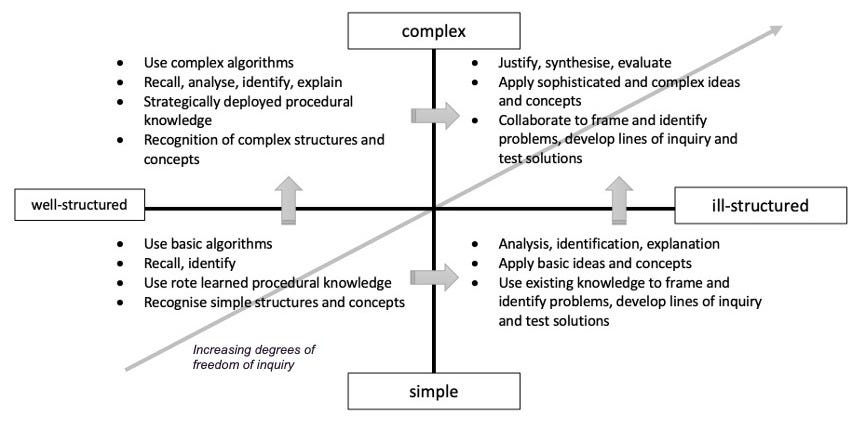
A busy but useful diagram
The diagram below is one I use to explain what kinds of thinking might be going on if we use the axes of well-structured/ill-structured and simple/complex.
Well-structured simple problems are quite straightforward and often use basic procedural or factual knowledge. They are suited to an ‘I do/we do/you do’ approach. Moving to more complex well-structured problems increases the demand on student thinking, but does not dramatically change the kinds of thinking on which they call. There is a bit of what we might think of as strategic thinking as they navigate complexity, and a deeper understanding is required.
Note: the arrows indicate that the skill on one quadrant are carried over into another.
Moving into ill-structured problems, however, creates a significant change in the types of thinking asked of students. Here they are more strategic, more evaluative, more generative and exploratory. They are also necessarily more collaborative, as alternative perspectives are sought, evaluated and justified.
Ill-structured problems are often excellent examples of Golden Tetrad cognitive activities, which I wrote about in an earlier post (as an alternative to Bloom’s Taxonomy). These activities focus on the core critical thinking skills: analyse, explain, evaluate and justify.
The more complex and ill-structured a problem, the greater the degrees of freedom of inquiry and the more rigor is required; in simple cases in the generative sense, in more complex cases, perhaps both the generative and restrictive senses.
So, if you want to create a rigorous curriculum, don’t fall for the siren call of stuffing it full of content. Rigour lies in thinking, and content is only relevant to rigour to the extent it makes cognitive demands on students.
Restrictive accounts of rigour alone do not create the thinkers we need for the future. It’s the generative thinkers that will make the difference.
Sometimes ‘I do/we do/you do’ just won’t do.
In my next post, I’ll talk about 3 critical questions to ask about thinking classrooms.





the room went silent when I said I don't believe in I do/We do/You do... thanks for echoing it back haha
It might be just me, but every time I hear the word ‘rigour’ in relation to anything in education, by brain always chimes in with ‘mortis’